
Математики открыли новый класс геометрических фигур
---
Квадрат, треугольник, ромб, круг и трапеция — одни из самых знакомых геометрических фигур. Однако, несмотря на эту кажущуюся полноту, природа продолжает удивлять нас. Недавно математики открыли новый класс геометрических фигур, способных полностью заполнять пространство в двух или трех измерениях. Известные как «мягкие клетки», эти формы встречаются в мышечных клетках и в раковинах моллюсков, таких как наутилус, с его изогнутыми трехмерными структурами.

Математики давно увлекаются плиткографией — наукой о том, как найти оптимальное расположение фигур на поверхности, не оставляя зазоров или наложений. Традиционно в геометрических решениях предпочтение отдавалось фигурам с определенными углами, таким как треугольники, шестиугольники и многогранники, чтобы полностью покрыть двухмерную плоскость.
Однако природа, похоже, следует совсем другим правилам.
Ален Гориели, профессор математического моделирования Оксфордского университета и соавтор нового исследования, пишет в пресс-релизе: «Природа не только не любит вакуум, но и, похоже, ненавидит острые углы». Примеры такого неприятия можно найти в раковине наутилуса, в поперечном сечении лука с его концентрическими слоями или даже в мышечных клетках, организованных в круговую мозаику. Поэтому математики столкнулись с серьезной проблемой, пытаясь расшифровать, как природа достигает такой геометрической сложности с помощью этих «мягких форм».
Вдохновившись тесселяциями Пенроуза, открытыми в 1980-х годах, команда под руководством Габора Домокоша из Будапештского университета технологии и экономики в сотрудничестве с математиками из Оксфордского университета нашла решение. В исследовании, опубликованном в журнале PNAS Nexus, ученые заново изучили периодические многоугольные тесселяции. Они выявили новый класс геометрических фигур: мягкие ячейки. По словам команды, эти фигуры «минимизируют количество острых углов и способны покрывать пространство без перекрытия».
 Мягкая версия усеченного октаэдра
Мягкая версия усеченного октаэдра
Два эксперимента с расходящимися результатами
В рамках своего исследования Домокос и его коллеги провели эксперименты с использованием новой алгоритмической модели. Они обнаружили, что в двумерном пространстве мягкие ячейки имеют только два угла. Подобная схема часто встречается в некоторых архитектурных конструкциях, таких как мышечные клетки и слои лука. Однако в трехмерном пространстве эти мягкие ячейки демонстрируют повышенную сложность.
«Мягкие клетки помогают объяснить, почему, когда вы смотрите на поперечное сечение раковины с камерами, вы видите углы, но не 3D-геометрию камер», — объясняет Домокош.
Изучая камеры наутилоидов, математики заметили острые углы в поперечных сечениях. Однако во внутренней трехмерной структуре они обнаружили более плавные геометрические фигуры, без определенных краев и с различными характеристиками укладки.
Домокош отмечает, что дальнейшее изучение раковин наутилусов оказалось неожиданным: их поперечные сечения напоминают мягкие клетки в 2D, но с двумя углами. Криштина Регос, соавтор исследования, говорит: «Несмотря на наличие двух углов на плоскости, мне показалось, что в трех измерениях углов нет».
Действительно, когда исследователи просмотрели детальные компьютерные томограммы, они обнаружили, что камеры наутилуса представляют собой мягкие клетки, заполняющие раковину без каких-либо углов.
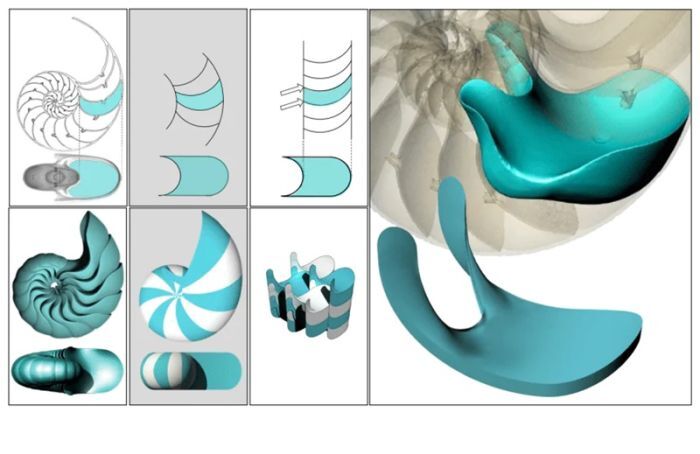
Поперечные сечения камерной оболочки показывают углы (слева), в то время как 3D-геометрия камер (справа) не показывает углов
«Мир многоугольных и многогранных тесселяций настолько увлекателен и богат, что математикам не пришлось расширять свою игровую площадку», — добавил Домокош. «Отсутствие острых углов и гладкая, сильно изогнутая геометрия делают мягкие клетки идеальными моделями для биологических структур, которые развивались в условиях полного или частичного ограничения пространства», — заключают исследователи.

Математики давно увлекаются плиткографией — наукой о том, как найти оптимальное расположение фигур на поверхности, не оставляя зазоров или наложений. Традиционно в геометрических решениях предпочтение отдавалось фигурам с определенными углами, таким как треугольники, шестиугольники и многогранники, чтобы полностью покрыть двухмерную плоскость.
Однако природа, похоже, следует совсем другим правилам.
Ален Гориели, профессор математического моделирования Оксфордского университета и соавтор нового исследования, пишет в пресс-релизе: «Природа не только не любит вакуум, но и, похоже, ненавидит острые углы». Примеры такого неприятия можно найти в раковине наутилуса, в поперечном сечении лука с его концентрическими слоями или даже в мышечных клетках, организованных в круговую мозаику. Поэтому математики столкнулись с серьезной проблемой, пытаясь расшифровать, как природа достигает такой геометрической сложности с помощью этих «мягких форм».
Вдохновившись тесселяциями Пенроуза, открытыми в 1980-х годах, команда под руководством Габора Домокоша из Будапештского университета технологии и экономики в сотрудничестве с математиками из Оксфордского университета нашла решение. В исследовании, опубликованном в журнале PNAS Nexus, ученые заново изучили периодические многоугольные тесселяции. Они выявили новый класс геометрических фигур: мягкие ячейки. По словам команды, эти фигуры «минимизируют количество острых углов и способны покрывать пространство без перекрытия».
 Мягкая версия усеченного октаэдра
Мягкая версия усеченного октаэдраДва эксперимента с расходящимися результатами
В рамках своего исследования Домокос и его коллеги провели эксперименты с использованием новой алгоритмической модели. Они обнаружили, что в двумерном пространстве мягкие ячейки имеют только два угла. Подобная схема часто встречается в некоторых архитектурных конструкциях, таких как мышечные клетки и слои лука. Однако в трехмерном пространстве эти мягкие ячейки демонстрируют повышенную сложность.
«Мягкие клетки помогают объяснить, почему, когда вы смотрите на поперечное сечение раковины с камерами, вы видите углы, но не 3D-геометрию камер», — объясняет Домокош.
Изучая камеры наутилоидов, математики заметили острые углы в поперечных сечениях. Однако во внутренней трехмерной структуре они обнаружили более плавные геометрические фигуры, без определенных краев и с различными характеристиками укладки.
Домокош отмечает, что дальнейшее изучение раковин наутилусов оказалось неожиданным: их поперечные сечения напоминают мягкие клетки в 2D, но с двумя углами. Криштина Регос, соавтор исследования, говорит: «Несмотря на наличие двух углов на плоскости, мне показалось, что в трех измерениях углов нет».
Действительно, когда исследователи просмотрели детальные компьютерные томограммы, они обнаружили, что камеры наутилуса представляют собой мягкие клетки, заполняющие раковину без каких-либо углов.

Поперечные сечения камерной оболочки показывают углы (слева), в то время как 3D-геометрия камер (справа) не показывает углов
«Мир многоугольных и многогранных тесселяций настолько увлекателен и богат, что математикам не пришлось расширять свою игровую площадку», — добавил Домокош. «Отсутствие острых углов и гладкая, сильно изогнутая геометрия делают мягкие клетки идеальными моделями для биологических структур, которые развивались в условиях полного или частичного ограничения пространства», — заключают исследователи.
Источник: salt.mediasalt.ru
Комментарии (0)
{related-news}
[/related-news]