Лишь экстраординарный мозг разберется, какой порядок действий в примере верный

Занятия математикой отлично задействуют мозг, способствуют развитию мышления. Нередко, чтобы решить сложную задачку, приходится проявлять изобретательность, находить нестандартный подход. При этом «царица наук» учит анализировать и строить логические цепочки. Вся эта работа не проходит бесследно. Ведь полученные навыки пригодятся не только в учебе, но и в повседневной жизни.

Хороший математик всегда обладает отличной памятью. У него прекрасно развито абстрактное мышление. Он всегда найдет способ, как решить насущные проблемы. Его терпение, усидчивость и настойчивость на высоте. Всё благодаря одной науке.

И сегодня редакция «Так Просто!» предлагает читателям снова немного позаниматься математикой. Ведь решить пример по действиям — это уже неплохая разминка для ума. А если таких примеров несколько, причем каждый имеет свои особенности? Тогда это уже целая тренировка, не иначе. Заодно проверь, насколько крепко ты дружишь с числами.

© Depositphotos
Решить пример по действиям

1. Первый пример не кажется сложным, но для разогрева вполне подойдет. Здесь есть все четыре основных арифметических операции. Разберешься, с чего начинать поиски решения? Какое действие выполнишь в первую очередь?
   
   ©
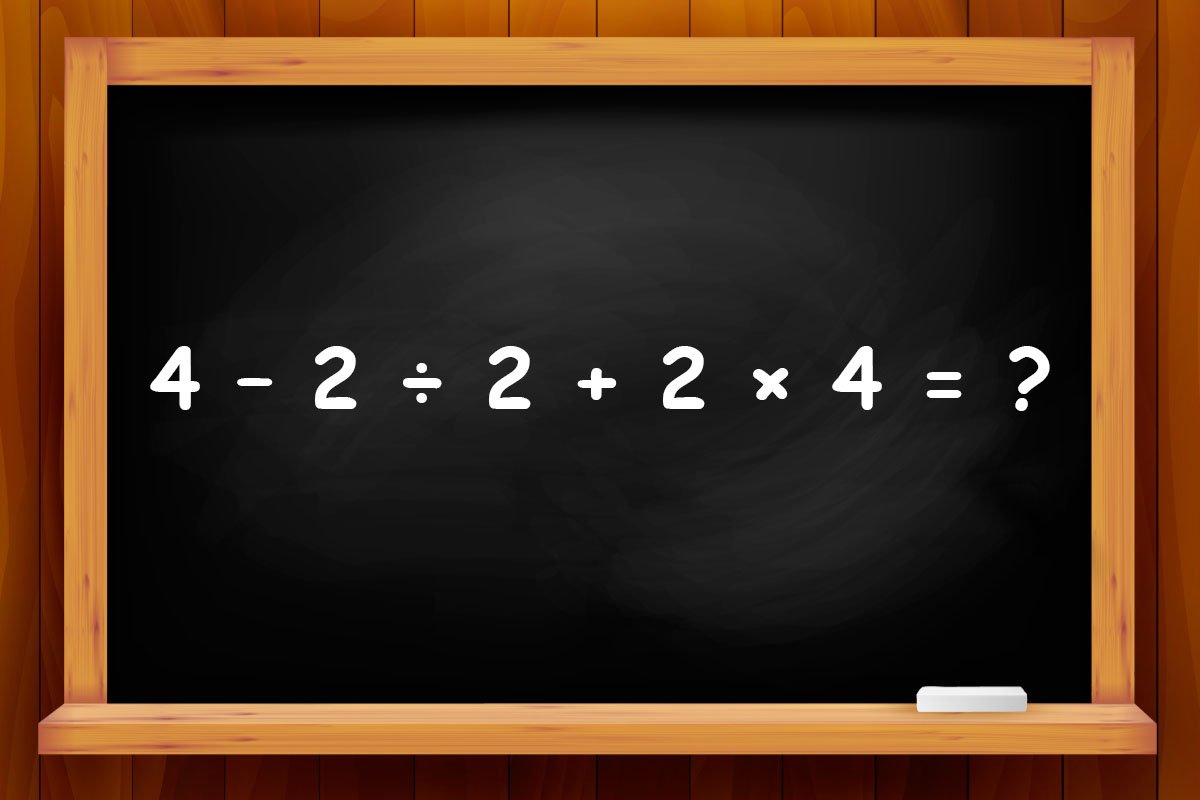2. Во втором задании придется делить на десятичную дробь. Помнишь, как это делается, или всё уже надежно позабыто? Вспоминай, ведь эти правила забывать не следует. Даже ученик средних классов справится, поэтому и тебе хорошо было бы не отставать.
   
   ©
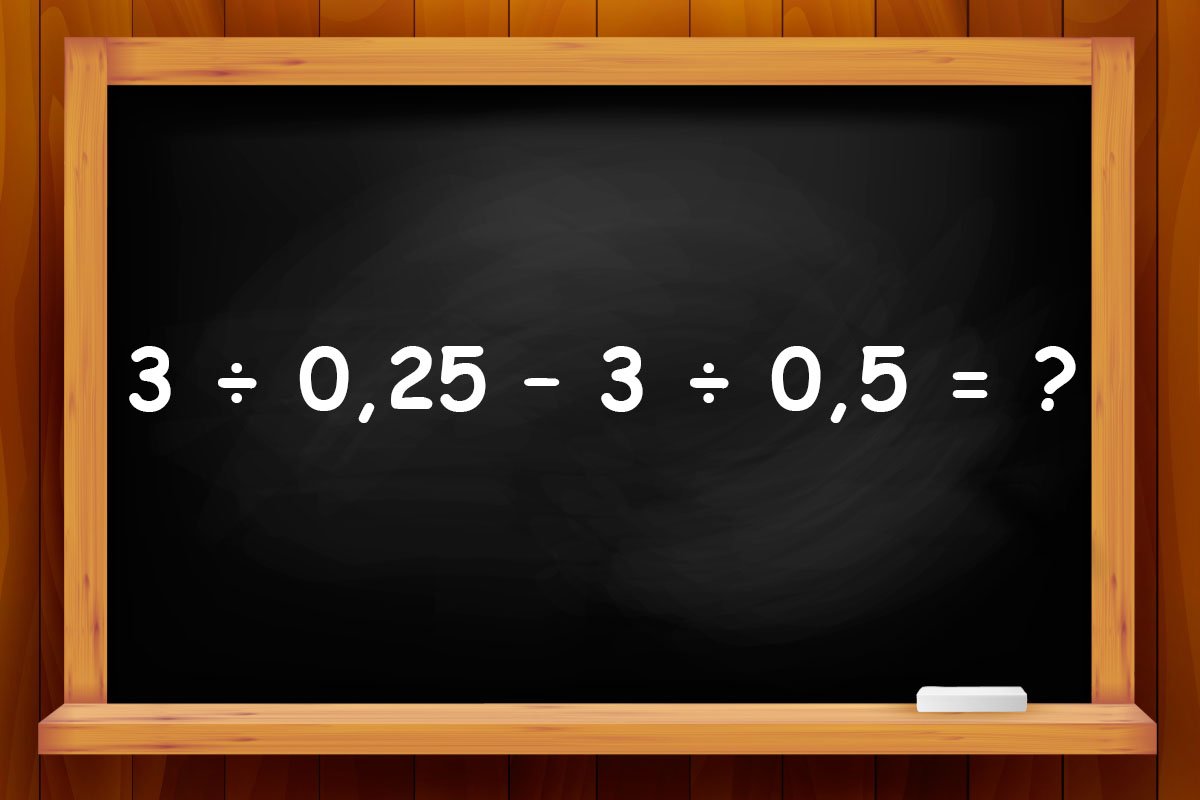3. Если помнишь, как находить корень квадратный, то это уже полдела. Останется совсем немного работы, чтобы найти решение. Поскорее разберись с последним примером, а затем сверься с нашими ответами во второй части статьи.
   
   ©

Подсказки и ответы

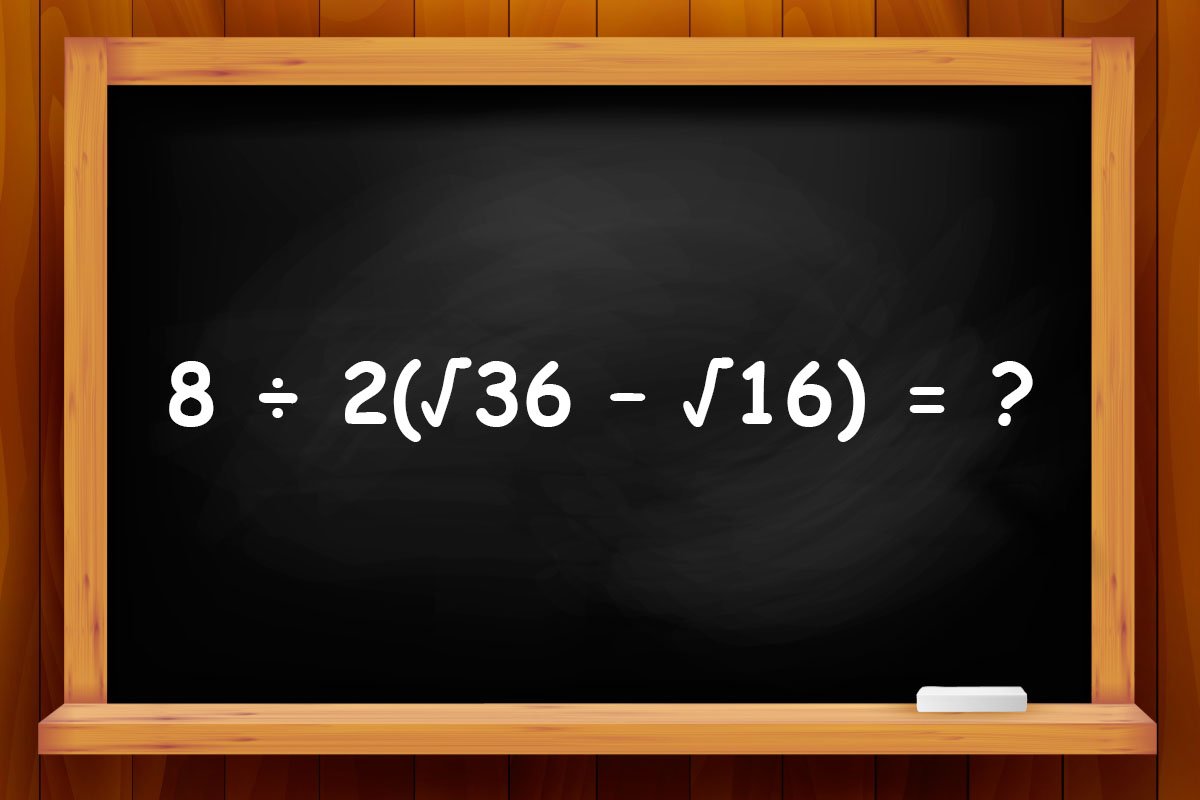1. Первым делом выполняем деление и умножение, а затем сложение и вычитание. В таком случае наш пример приобретает следующий вид: 4 – 2 ÷ 2 + 2 × 4 = 4 – 1 + 8 = 11.
   
   ©
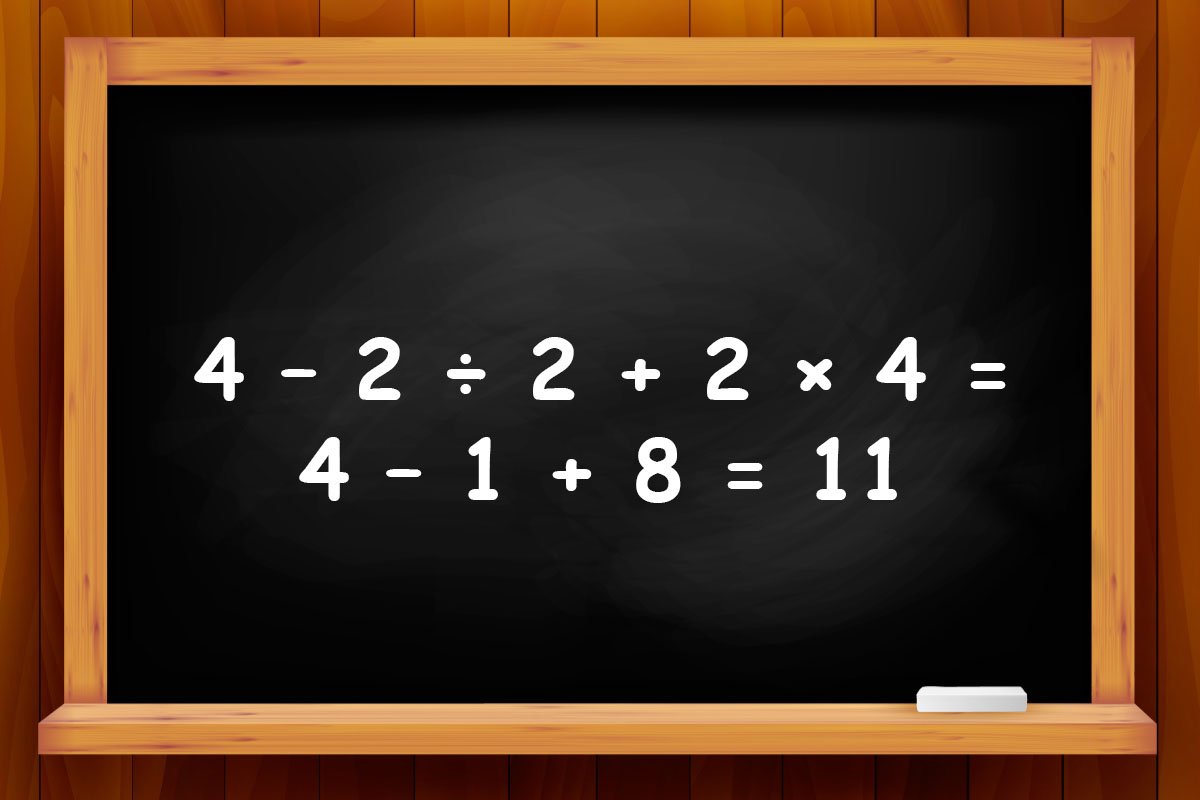2. Поделить на 0,25 — это всё равно, что умножить на 4. А поделить на 0,5 — это то же самое, что умножить на 2. Тогда получаем 3 ÷ 0,25 – 3 ÷ 0,5 = 3 × 4 – 3 × 2 = 12 – 6 = 6.
   
   ©
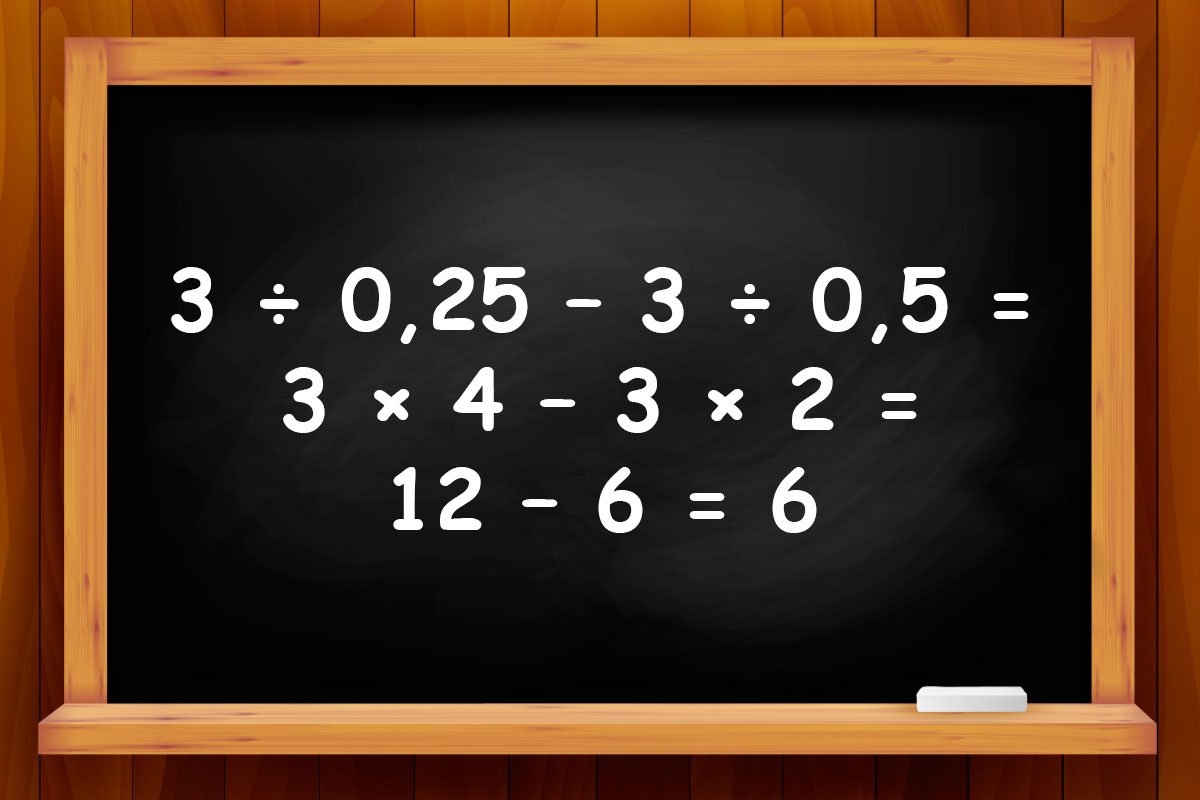3. В первую очередь нужно извлечь квадратный корень из чисел 36 и 16. Почти каждый школьник знает, что √36 = 6, а √16 = 4. Тогда наш пример станет куда понятнее. Ведь 8 ÷ 2(√36 – √16) = 8 ÷ 2(6 – 4) = 8 ÷ 2 × 2 = 4 × 2 = 8.
   
   ©

Признавайся, удалось ли решить всё правильно. Делись своими размышлениями и вариантами ответов в комментариях с другими читателями. Также пробуй решить математические задачки. Или же находи подход к хитрым головоломкам, которые способны озадачить любого взрослого человека с высшим образованием.

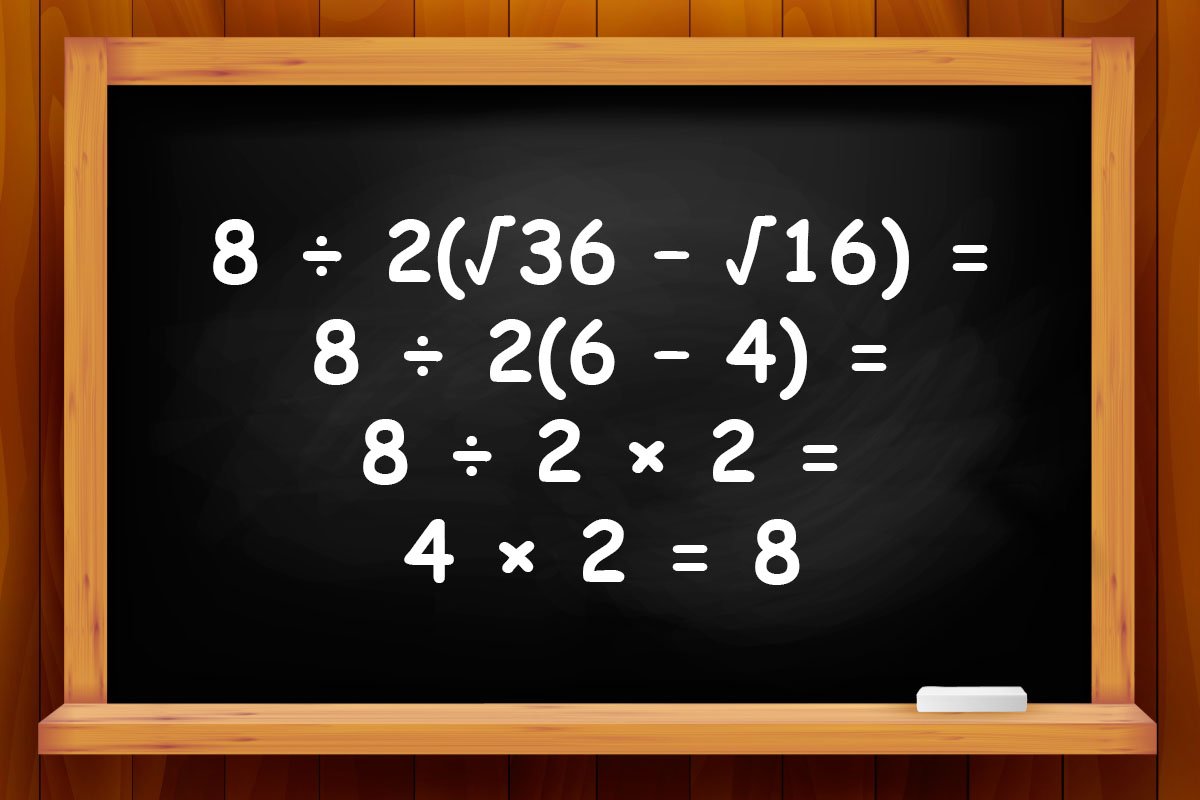Источник: takprosto.cc

уникальные шаблоны и модули для dle